八个常见的机器学习算法的计算复杂度总结

偷偷努力，悄无声息地变强，然后惊艳所有人！哈哈，小伙伴们又来学习啦~今天我将给大家介绍《八个常见的机器学习算法的计算复杂度总结》，这篇文章主要会讲到等等知识点，不知道大家对其都有多少了解，下面我们就一起来看一吧！当然，非常希望大家能多多评论，给出合理的建议，我们一起学习，一起进步！

计算的复杂度是一个特定算法在运行时所消耗的计算资源(时间和空间)的度量。

计算复杂度又分为两类:

1、时间复杂度

时间复杂度不是测量一个算法或一段代码在某个机器或者条件下运行所花费的时间。时间复杂度一般指时间复杂性，时间复杂度是一个函数，它定性描述该算法的运行时间，允许我们在不运行它们的情况下比较不同的算法。例如，带有O(n)的算法总是比O(n²)表现得更好，因为它的增长率小于O(n²)。

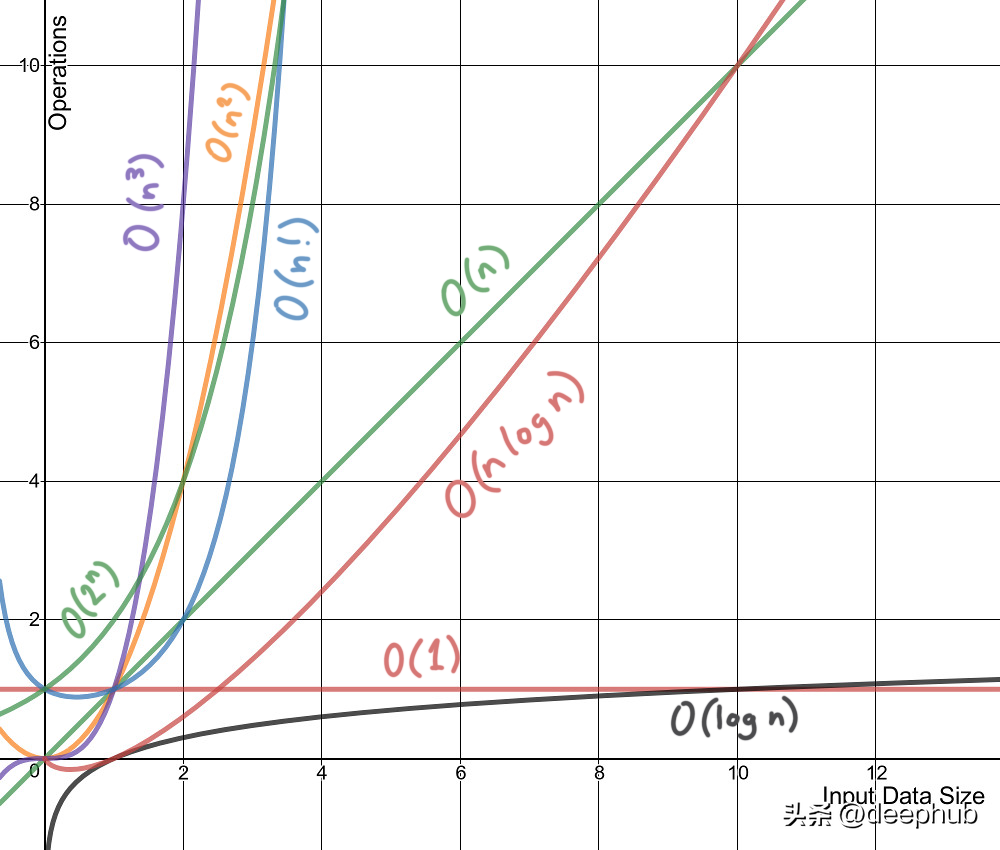
2、空间复杂度

就像时间复杂度是一个函数一样，空间复杂度也是如此。 从概念上讲，它与时间复杂度相同，只需将时间替换为空间即可。 维基百科将空间复杂度定义为：

算法或计算机程序的空间复杂度是解决计算问题实例所需的存储空间量，以特征数量作为输入的函数。

下面我们整理了一些常见的机器学习算法的计算复杂度。

1、线性回归

• n= 训练样本数，f = 特征数
• 训练时间复杂度：O(f²n+f³)
• 预测时间复杂度：O(f)
• 运行时空间复杂度：O(f)

2、逻辑回归：

• n= 训练样本数，f = 特征数
• 训练时间复杂度：O(f*n)
• 预测时间复杂度：O(f)
• 运行时空间复杂度：O(f)

3、支持向量机：

• n= 训练样本数，f = 特征数，s= 支持向量的数量
• 训练时间复杂度：O(n²) 到 O(n³)，训练时间复杂度因内核不同而不同。
• 预测时间复杂度：O(f) 到 O(s*f):线性核是 O(f)，RBF 和多项式是 O(s*f)
• 运行时空间复杂度：O(s)

4、朴素贝叶斯：

• n= 训练样本数，f = 特征数，c = 分类的类别数
• 训练时间复杂度：O(n*f*c)
• 预测时间复杂度：O(c*f)
• 运行时空间复杂度：O(c*f)

5、决策树：

• n= 训练样本数，f = 特征数，d = 树的深度，p = 节点数
• 训练时间复杂度：O(n*log(n)*f)
• 预测时间复杂度：O(d)
• 运行时空间复杂度：O(p)

6、随机森林：

• n= 训练样本数，f = 特征数，k = 树的数量，p=树中的节点数，d = 树的深度
• 训练时间复杂度：O(n*log(n)*f*k)
• 预测时间复杂度：O(d*k)
• 运行时空间复杂度：O(p*k)

7、K近邻：

n= 训练样本数，f = 特征数，k= 近邻数

Brute：

• 训练时间复杂度：O(1)
• 预测时间复杂度：O(n*f+k*f)
• 运行时空间复杂度：O(n*f)

kd-tree：

• 训练时间复杂度：O(f*n*log(n))
• 预测时间复杂度：O(k*log(n))
• 运行时空间复杂度：O(n*f)

8、K-means 聚类：

• n= 训练样本数，f = 特征数，k= 簇数，i = 迭代次数
• 训练时间复杂度：O(n*f*k*i)
• 运行时空间复杂度：O(n*f+k*f)

今天关于《八个常见的机器学习算法的计算复杂度总结》的内容介绍就到此结束，如果有什么疑问或者建议，可以在golang学习网公众号下多多回复交流；文中若有不正之处，也希望回复留言以告知！